【AtCoder】Pythonで使いこなすUnion-Find木

2021.06.23

2024.03.24

競技プログラミング

AtCoderPythonUnion-Find木

本ページはAmazonアフィリエイトのリンクを含みます。

はじめに

Union-Find木について、どんなものなのか、AtCoderなどではどんな問題で使うのか、Pythonで実装したサンプルコードについて紹介していきます。

実際のAtCoderで利用したプログラムも掲載しています。

Union-Find木とは

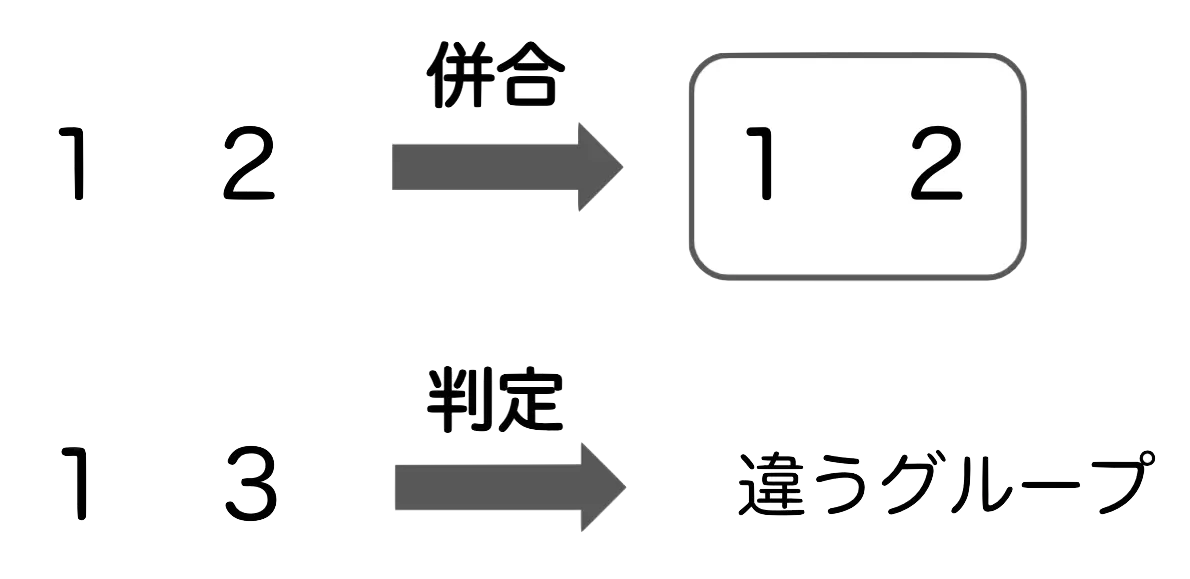
Union-Find木とは、グループが互いに重ならない(素集合)ようにグループ分けを管理するデータ構造です。

以下のことが効率的にできます。

併合：グループ同士をまとめる
判定：要素同士が同じグループに属しているか

Union-Find木は、名前の通り木を使って実現します。各要素がノード、グループが木となります。

初期化

まずはじめは、n個の要素を用意します。

このときはそれぞれのノードは木になっていません。

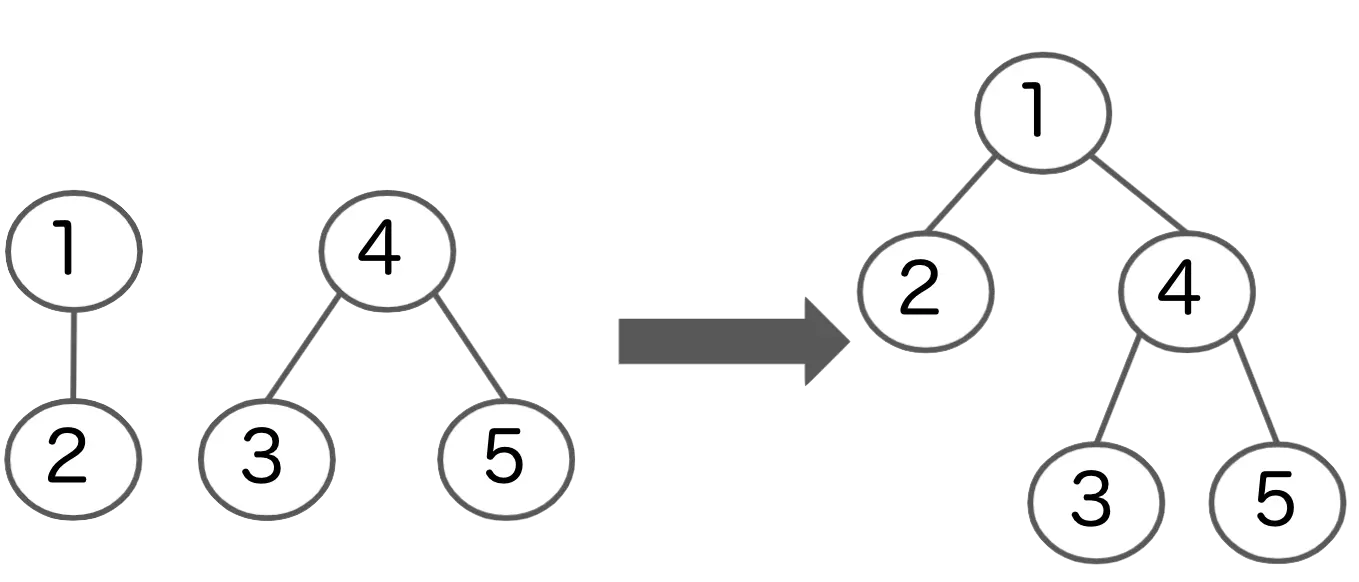
併合

2つのグループをまとめて1つにします。

片方の根にもう片方の木の根に辺を張り、1つの木にします。

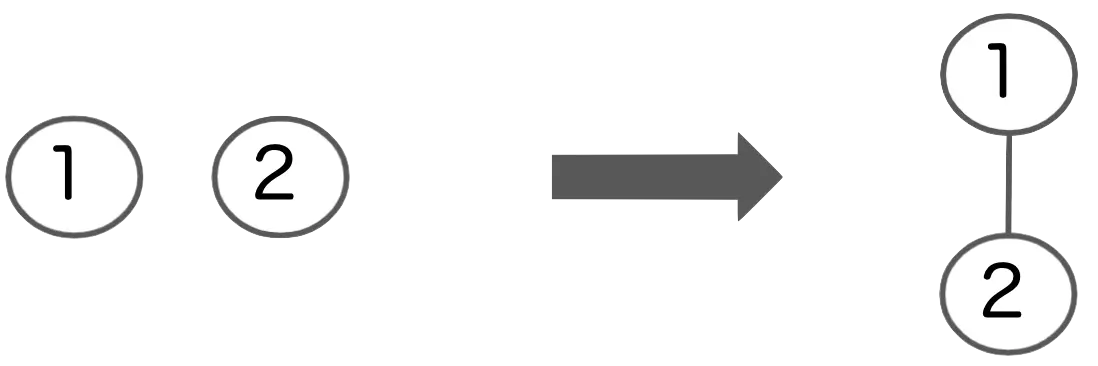
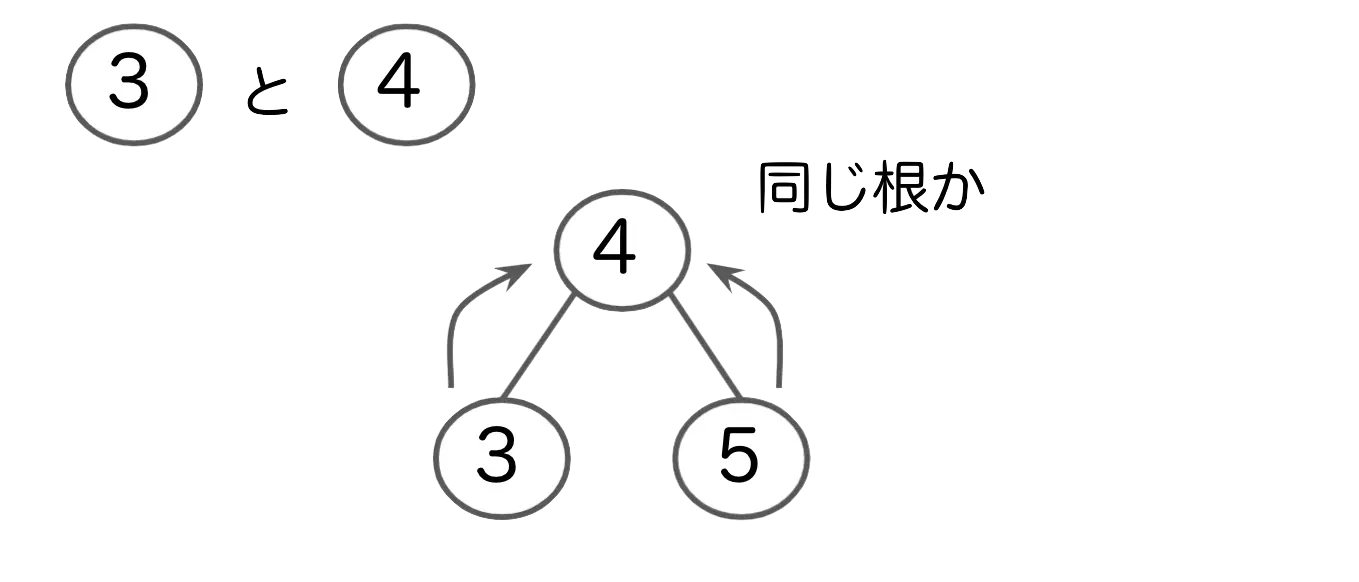
判定

同じグループかの判定は木をたどり、同じ根になるかどうかで判定します。

使いどころ

AtCoderなどでは、グループ分けをするような問題で使えることが多いですが、一度覚えるとなんでもできるのではないかと思ってしまうので、注意が必要です。

逆にUninon-Find木で考えると簡単になるのに、思いつかなかったという問題もあったので、問題の定式化が重要になるかと思います。

Union-Find木のサンプルコード

Union-Find木のサンプルコードになります。

クラスとして実装しているので、利用する場合はそのままコピペで使えます。

1from collections import defaultdict
2
3
4class UnionFind():
5    """
6    Union Find木クラス
7
8    Attributes
9    --------------------
10    n : int
11        要素数
12    root : list
13        木の要素数
14        0未満であればそのノードが根であり、添字の値が要素数
15    rank : list
16        木の深さ
17    """
18
19    def __init__(self, n):
20        """
21        Parameters
22        ---------------------
23        n : int
24            要素数
25        """
26        self.n = n
27        self.root = [-1]*(n+1)
28        self.rank = [0]*(n+1)
29
30    def find(self, x):
31        """
32        ノードxの根を見つける
33
34        Parameters
35        ---------------------
36        x : int
37            見つけるノード
38
39        Returns
40        ---------------------
41        root : int
42            根のノード
43        """
44        if(self.root[x] < 0):
45            return x
46        else:
47            self.root[x] = self.find(self.root[x])
48            return self.root[x]
49
50    def unite(self, x, y):
51        """
52        木の併合
53
54        Parameters
55        ---------------------
56        x : int
57            併合したノード
58        y : int
59            併合したノード
60        """
61        x = self.find(x)
62        y = self.find(y)
63
64        if(x == y):
65            return
66        elif(self.rank[x] > self.rank[y]):
67            self.root[x] += self.root[y]
68            self.root[y] = x
69        else:
70            self.root[y] += self.root[x]
71            self.root[x] = y
72            if(self.rank[x] == self.rank[y]):
73                self.rank[y] += 1
74
75    def same(self, x, y):
76        """
77        同じグループに属するか判定
78
79        Parameters
80        ---------------------
81        x : int
82            判定したノード
83        y : int
84            判定したノード
85
86        Returns
87        ---------------------
88        ans : bool
89            同じグループに属しているか
90        """
91        return self.find(x) == self.find(y)
92
93    def size(self, x):
94        """
95        木のサイズを計算
96
97        Parameters
98        ---------------------
99        x : int
100            計算したい木のノード
101
102        Returns
103        ---------------------
104        size : int
105            木のサイズ
106        """
107        return -self.root[self.find(x)]
108
109    def roots(self):
110        """
111        根のノードを取得
112
113        Returns
114        ---------------------
115        roots : list
116            根のノード
117        """
118        return [i for i, x in enumerate(self.root) if x < 0]
119
120    def group_size(self):
121        """
122        グループ数を取得
123
124        Returns
125        ---------------------
126        size : int
127            グループ数
128        """
129        return len(self.roots())
130
131    def group_members(self):
132        """
133        全てのグループごとのノードを取得
134
135        Returns
136        ---------------------
137        group_members : defaultdict
138            根をキーとしたノードのリスト
139        """
140        group_members = defaultdict(list)
141        for member in range(self.n):
142            group_members[self.find(member)].append(member)
143        return group_members

使い方

以下のようにUnion-Find木で併合や判定が可能です。

1n = 5
2uf = UnionFind(n)
3uf.unite(1, 2)
4uf.unite(4, 3)
5uf.unite(4, 5)
6
7uf.find(1)
8uf.find(4)
9
10uf.same(1, 2)
11uf.same(1, 3)

AtCoderのサンプル問題

ARC106 B問題

B - Values

AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.

N頂点M辺の無向グラフが与えられ、それぞれの頂点を $a_{i}$ から $b_{i}$ に変更可能か判定する問題です。

各連結成分ごとの総和で判定するため、Union-Find木でグループ分けし、グループごとの総和を求めています。

1import numpy as np
2
3n, m = map(int, input().split())
4a = np.array(list(map(int, input().split())))
5b = np.array(list(map(int, input().split())))
6c = []
7d = []
8for _ in range(m):
9    tmp_c, tmp_d = map(int, input().split())
10    c.append(tmp_c-1)
11    d.append(tmp_d-1)
12
13uf = UnionFind(n)
14for i in range(m):
15    uf.unite(c[i], d[i])
16
17for g in uf.group_members().values():
18    if sum(a[g]) != sum(b[g]):
19        print('No')
20        exit()
21
22print('Yes')

ABC177 D問題

D - Friends

AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.

N人のM個の関係性（友達かどうか）が与えられ、友達の友達は友達のとき、N人を同じグループに友達がいない最小のグループ数を求めます。

友達同士のグループを作り、友達同士が最大のグループを求める必要があるのでUnion-Find木でグループ分けし、それぞれのグループの人数で判定しています。

1n, m = map(int, input().split())
2A = []
3B = []
4for _ in range(m):
5    a, b = map(int, input().split())
6    A.append(a-1)
7    B.append(b-1)
8
9uf = UnionFind(n)
10
11for i in range(m):
12    uf.unite(A[i], B[i])
13
14ans = 0
15for g in uf.group_members().values():
16    g_size = len(g)
17    if g_size > ans:
18        ans = g_size
19
20print(ans)

ABC206 D問題

D - KAIBUNsyo

AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.

N項からなる数列を回文に変える問題です。

回文になる組み合わせ（同じになるべき数字同士）のグループに分けるのにUnion-Find木を利用します。 Union-Find木で解くと考えるまでが大変ですが、解き方がわかれば簡単に実装できます。

1n = int(input())
2A = list(map(int, input().split()))
3uf = UnionFind(2 * 10**5 + 1)
4
5ans = 0
6for i in range(n//2):
7    uf.unite(A[i], A[-(i+1)])
8
9for g in uf.group_members().values():
10    ans += len(g)-1
11
12print(ans)