はじめに
AtCoderで出てくる素数に関する問題で使えそうなPythonのサンプルコードをまとめました。
素数に関するアルゴリズムを応用するような問題は、これらのコードを変更することで対応できると思います。
素数に関する問題
AtCoderなどで出てくる素数に関する問題は主に下記3つぐらいかと思います。
- 素数判定
- 素数列挙
- 素因数分解
これら3つのサンプルコードについて紹介します。
素数判定
まずはある数が素数かどうかを判定する問題になります。
判定する数が1つであれば\(\sqrt{n}\)までの整数で割り切れるかどうかで、ある程度の問題は判定できます。
サンプルコード
import math
def is_prime(n):
sqrt_n = math.ceil(math.sqrt(n))
for i in range(2, sqrt_n):
if n % i == 0:
return False
return True以下のように使えます。
n = int(input())
print(is_prime(n))53
True素数列挙
複数の数を素数かどうか判定して列挙するような問題はより高速は方法が必要になります。
素数の列挙にはエラトステネスの篩を利用します。
エラトステネスの篩は、N以下の素数を列挙するのに、2以上N以下の整数をまずは書き出します。その中から2から順に倍数を取り除いていくという処理を繰り返すことで素数のみにするアルゴリズムです。
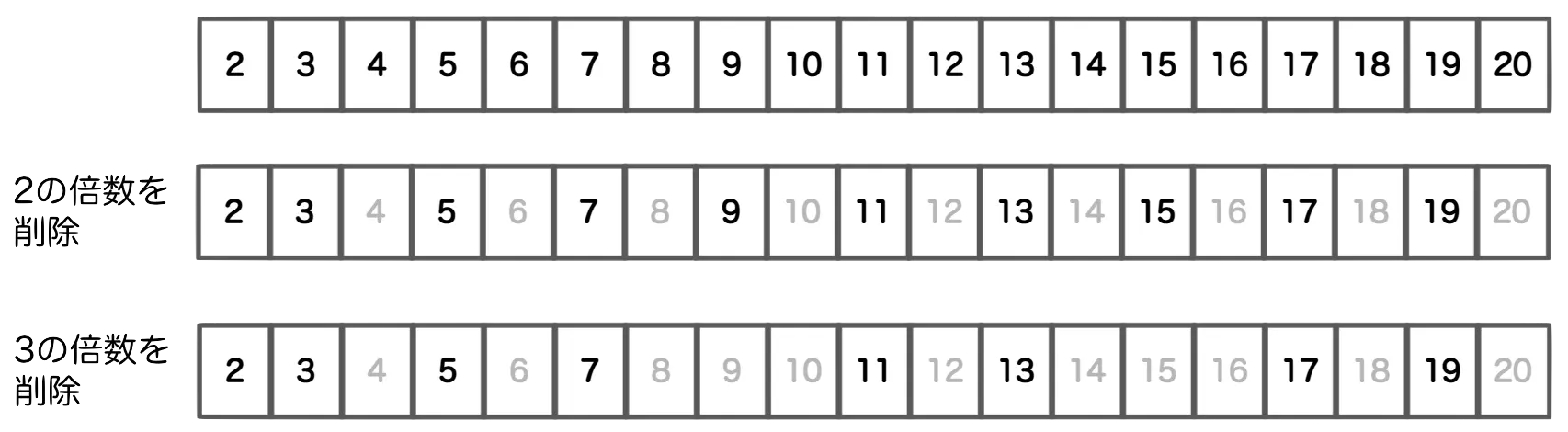
N以下の素数の列挙
サンプルコード
import math
def sieve_of_eratosthenes(n):
prime = [True for i in range(n+1)]
prime[0] = False
prime[1] = False
sqrt_n = math.ceil(math.sqrt(n))
for i in range(2, sqrt_n):
if prime[i]:
for j in range(2*i, n+1, i):
prime[j] = False
return prime以下のように利用することで素数の列挙、素数の数を求めることができます。
n = int(input())
# 素数の列挙
prime = sieve_of_eratosthenes(n)
for p in range(n+1):
if prime[p]:
print(p, end=' ')
# 素数の数
print(sum(prime))11
2 3 5 7 11
5特定の区間の素数
エラトステネスの篩を利用することで特定の区間の素数の列挙も可能です。
区間\([a, b]\)の素数を列挙する場合、\(b\)以下の素因数として考えられるのは\(\sqrt{b}\)なので、\([2, \sqrt{b}]\)の区間の素数で\([a ,b]\)の整数からその倍数を取り除いていくことで区間\([a, b]\)の素数を列挙することができます。
サンプルコード
import math
def segment_sieve(a, b):
sqrt_b = math.ceil(math.sqrt(b))
prime_small = [True for i in range(sqrt_b)]
prime = [True for i in range(b-a+1)]
for i in range(2, sqrt_b):
if prime_small[i]:
for j in range(2*i, sqrt_b, i):
prime_small[j] = False
for j in range((a+i-1)//i*i, b+1, i):
print('j: ', j)
prime[j-a] = False
return prime以下のように利用することで素数の列挙と素数の数が求められます。
a, b = map(int, input().split())
seg_prime = segment_sieve(a, b)
for p in range(b-a+1):
if seg_prime[p]:
print(p+a, end=' ')
print(sum(seg_prime))22 37
23 29 31 37
4素因数分解
素因数分解は素数判定とほとんど同じで、2から\(\sqrt{n}\)まで順番に整数で割り切れるだけ割るという処理を繰り返します。
サンプルコード
import math
def factorization(n):
fact = []
for i in range(2, math.ceil(math.sqrt(n))):
if n % i == 0:
cnt = 0
while n % i == 0:
cnt += 1
n //= i
fact.append([i, cnt])
if n != 1:
fact[n] = 1
return fact以下のように利用すると、[素因数, 指数]の形式で求めることができます。
n = int(input())
print(factorization(n))24
[[2, 3], [3, 1]]
