【AtCoder】Pythonで使いこなす深さ優先探索・幅優先探索

2021.07.02

2024.03.24

競技プログラミング

AtCoderPython幅優先探索深さ優先探索

本ページはAmazonアフィリエイトのリンクを含みます。

はじめに

深さ優先探索と幅優先探索について、どんなものなのか、典型的な問題とそのサンプルコードを紹介したいと思います。

深さ優先探索と幅優先探索の実装については、問題ごとに実装を変える必要があるので注意してください。

今回扱う問題は、AtCoderのAtCoder Typical Contestからサンプル問題を選びました。

深さ優先探索とは

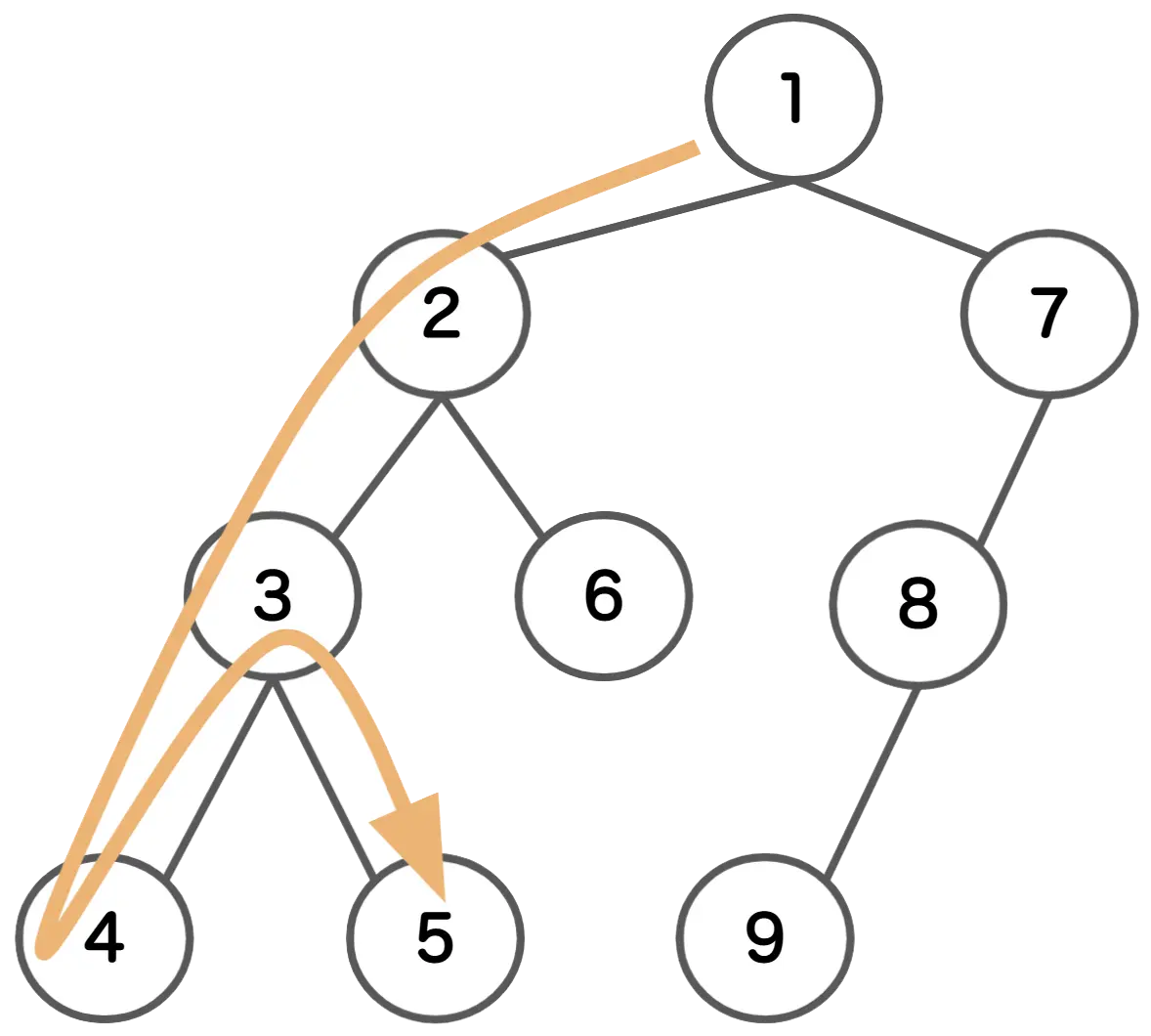
深さ優先探索(DFS: Depth-First Search)とは、深さ（それ以上の状態に繊維できないまで）を優先的に探索する手法です。

初期状態から遷移し、それ以上遷移できなくなったら、1つ前の状態に戻り、さらに探索していない状態へ遷移することを繰り返します。

状態の遷移を木構造で考えると深さを優先していることがわかりやすいです。最初の状態（根）から深さ方向に探索していき、状態の遷移を繰り返すことで全ての状態を列挙できます。

典型的な問題とサンプルコード

A - 深さ優先探索

AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.

スタートからゴールまで辿り着けるかを判定する問題です。

スタートから辿り着ける場所を全て列挙して、その中にゴールがあるか確認すればいいので、深さ優先探索でスタートから探索してゴールに辿り着けるか判定します。

深さ優先探索は再起関数で簡単に書けます。

Pythonでは再起呼び出しの上限があり、デフォルトでは1000になっています。AtCoderのテストケースでは足りないので、上限の設定をしておく必要があります。

1>>> import sys
2>>> sys.getrecursionlimit()
31000

1import sys
2sys.setrecursionlimit(10**7) # 再起回数の設定
3
4H, W = map(int, input().split())
5maze = [list(input()) for h in range(H)]
6
7for h in range(H):
8    for w in range(W):
9        if maze[h][w] == "s":
10            sx, sy = h, w
11
12
13# 深さ優先探索
14def dfs(x, y):
15    # 範囲外や壁の場合は終了
16    if y >= W or y < 0 or x >= H or x < 0 or maze[x][y] == '#':
17        return
18
19    # ゴールに辿り着ければ終了
20    if maze[x][y] == 'g':
21        print('Yes')
22        exit()
23
24    maze[x][y] = '#' # 確認したルートは壁にしておく
25
26    # 上下左右への移動パターンで再起していく
27    dfs(x+1, y)
28    dfs(x-1, y)
29    dfs(x, y+1)
30    dfs(x, y-1)
31
32
33dfs(sx, sy) # スタート位置から深さ優先探索
34print('No')

幅優先探索とは

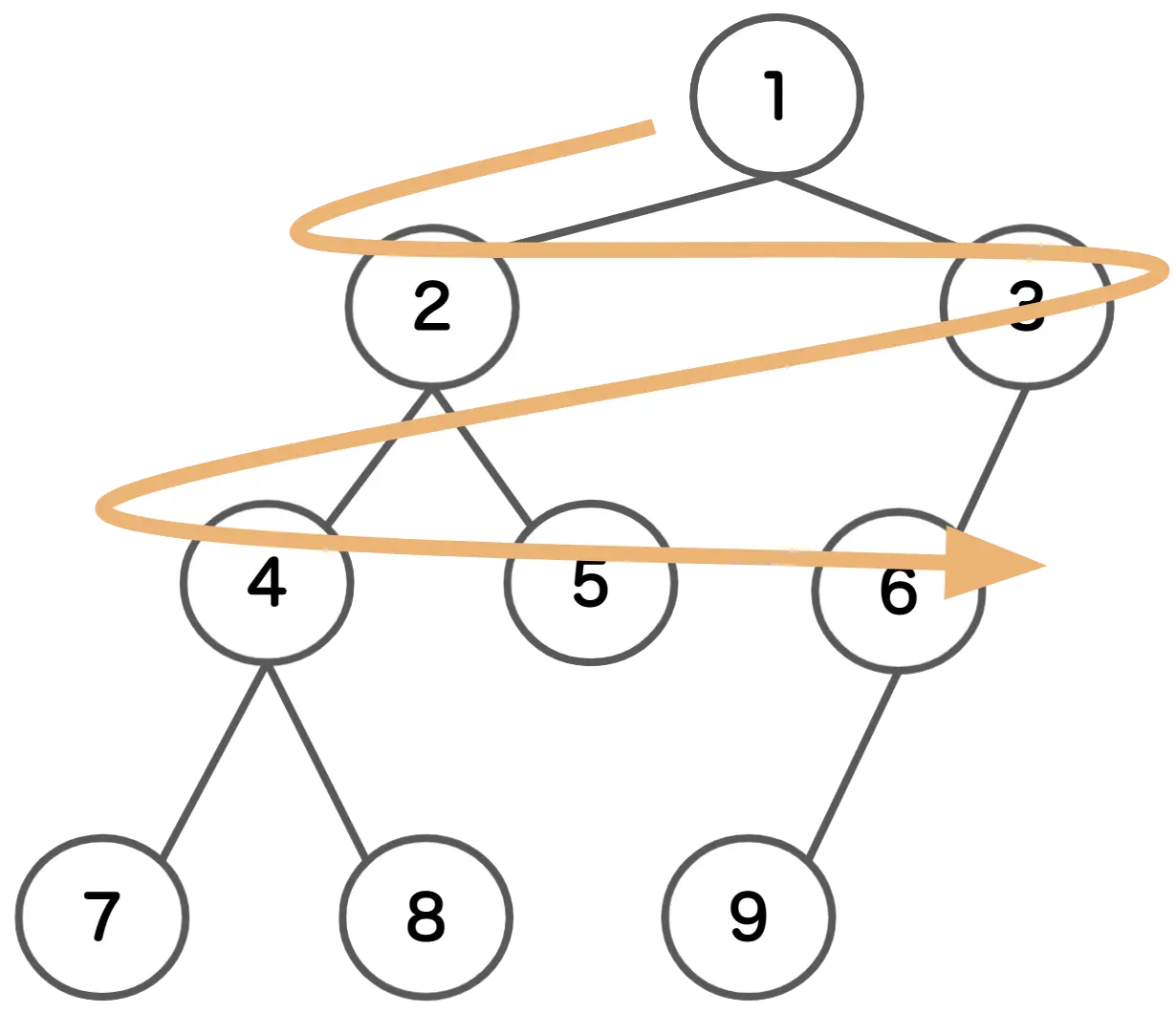
幅優先探索(BFS: Breadth-First Search)とは、幅（最初の状態から近い状態）を優先的に探索する手法です。

最初の状態から1回の遷移でいける全ての状態、2回の遷移でいける全ての状態と繰り返して全ての状態を列挙できます。

木構造で考えると同じ深さにあるノードを根に近い方から探索するというイメージになります。根に近い方から探索するため、最短経路や最小手数などの問題も求めることができます。

典型的な問題とサンプルコード

A - 幅優先探索

AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.

迷路でのスタートからゴールの最小移動手数を求める問題です。

スタートから1回で辿り着けるマス、2回で辿り着けるマス...と全てのマスに対してスタートから最短手数で辿り着ける数を求めながら最終的にゴールのマスの最小手数を求めます。

再入れ先出しのキューというデータ構造を使うと実装が簡単です。 Pythonではdepue（両端キュー）を利用します。

1from collections import deque
2
3R, C = map(int, input().split())
4sx, sy = map(int, input().split())
5gx, gy = map(int, input().split())
6maze = [list(input()) for h in range(R)]
7
8sx, sy, gx, gy = sx-1, sy-1, gx-1, gy-1
9
10dist = [[10**4 for i in range(C)] for j in range(R)] # 各マスの最小手数
11
12for r in range(R):
13    for c in range(C):
14        if maze[r][c] == '#':
15            dist[r][c] = -1 # 壁は-1
16
17dist[sx][sy] = 0
18
19que = deque()
20que.append([sx, sy])
21d = [[1, 0], [-1, 0], [0, 1], [0, -1]] # 移動方向のリスト
22
23# 幅優先探索
24while que:
25    x, y = que.popleft() # キューから取り出し
26
27    # 現在位置から上下左右に探索
28    for i, j in d:
29        if x+i >= R or x+i < 0 or y+j >= C or y+j < 0: # 範囲外
30            continue
31        if maze[x+i][y+j] == '#': # 壁
32            continue
33        if dist[x+i][y+j] != 10**4: # すでに最小手数確定済み
34            continue
35
36        dist[x+i][y+j] = dist[x][y] + 1
37
38        que.append([x+i, y+j]) # 次のマスをキューに格納
39
40print(dist[gx][gy])