機械学習で使われる評価関数まとめ

2021.05.19

2024.03.24

機械学習

Python評価関数

本ページはAmazonアフィリエイトのリンクを含みます。

はじめに

Qiitaで投稿した「機械学習で使われる評価関数まとめ」に追記した内容になります。

評価関数（評価指標）についてあやふやな理解だったので、代表的な評価関数をまとめてみました。

評価関数とはそもそもどんなものなのか、それぞれの評価関数はどんな意味を持つのか、実際に使う時のサンプルコードを簡単にまとめています。

評価関数に特化した本としては、下記がおすすめです。

Amazonで見る

評価関数とは

評価関数とは学習させたモデルの良さを測る指標を指します。

目的関数との違い

機械学習を勉強していると、目的関数や損失関数、コスト関数などいろいろな名前を目にします。

まずは、目的関数との違いについて確認します。

目的関数
- モデルの学習で最適化される関数
- 微分できる必要がある

つまり、学習中に最適化されるのが目的関数、学習後に良さを確認するための指標が評価関数ということになります。

損失関数、コスト関数、誤差関数は目的関数の一部になるそうです。（いくつか議論がありそうなのですが、ほとんど同じものと考えても良さそうです。）

回帰

まずは、回帰問題の評価関数について、まとめていきます。

サンプルデータで扱う真の値と予測の値は以下のようになります。

1y_true = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
2y_pred = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 5.0]

MAE(Mean Absolute Error)

平均絶対誤差。真の値と予測の値の差の絶対値の平均を表します。

外れ値の影響を小さく評価

\textrm{MAE} = \frac{1}{N}\sum_{i=1}^{N}|y_{i}-\hat{y}_{i}|

\begin{align} N & : \textrm{レコード数} \nonumber \\ y_{i} & : \textrm{i番目のレコードの真の値} \nonumber \\ \hat{y}_{i} & : \textrm{i番目のレコードの予測値} \nonumber \end{align}

1from sklearn.metrics import mean_absolute_error
2mean_absolute_error(y_true, y_pred)
3# => 0.5

MAPE(Mean Absolute Percentage Error)

平均絶対パーセント誤差。真の値と予測の値の差を真の値で割ったの絶対値の平均を表します。

誤差を割合で表現
予測する値のスケールが異なる誤差を比較しやすい
真の値に0が含まれる場合は利用できない（0で割ることになってしまう）

\textrm{MAPE} = \frac{100}{N}\sum_{i=1}^{N}|\frac{y_{i}-\hat{y}_{i}}{y_{i}}|

直接計算できないため、numpyを利用します。

1import numpy as np
2y_true, y_pred = np.array(y_true), np.array(y_pred)
3np.mean(np.abs((y_true - y_pred) / y_true)) * 100
4# => 5.0

MSE(Mean Squared Error)

平均二乗誤差。真の値と予測の値の差を二乗した平均を表します。

外れ値の影響を大きく評価
単位が目的変数の二乗

\textrm{MSE} = \frac{1}{N}\sum_{i=1}^{N}(y_{i}-\hat{y}_{i})^{2}

1from sklearn.metrics import mean_squared_error
2mean_squared_error(y_true, y_pred)
3# => 2.5

RMSE(Root Mean Squared Error)

平均平方二乗誤差。真の値と予測の値の差を二乗した平均を表します。

外れ値の影響を大きく評価
単位が目的変数と同じ

\textrm{RMSE} = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(y_{i}-\hat{y}_{i})^{2}}

scikit-learnのモジュールでは直接計算できないため、mean_squared_errorから計算する必要があります。

1from sklearn.metrics import mean_squared_error
2import numpy as np
3np.sqrt(mean_squared_error(y_true, y_pred))
4# => 1.5811388300841898

RMSLE(Root Mean Squared Logarithmic Error)

真の値と予測の値の対数をそれぞれとったあとの差を二乗した平均を表します。

目的変数のとりうる値の範囲が広いデータに利用
差を比率として表現

\textrm{RMSLE} = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(\log (1+y_{i})-\log (1+\hat{y}_{i}))^{2}}

1from sklearn.metrics import mean_squared_log_error
2import numpy as np
3np.sqrt(mean_squared_log_error(y_true, y_pred))
4# => 0.19167697106586185

決定係数

$\textrm{R}^{2}$

回帰分析の当てはまりの良さを表します。

目的変数のスケールに依存せず評価可能
0から1の値をとる

\textrm{R}^{2} = 1 - \frac{\sum_{i=1}^{N}(y_{i}-\hat{y_{i}})^{2}}{\sum_{i=1}^{N}(y_{i}-\bar{y_{i}})^{2}}

\bar{y} = \frac{1}{N}\sum_{i=1}^{N}y_{i}

1from sklearn.metrics import r2_score
2r2_score(y_true, y_pred)
3# => 0.696969696969697

二値分類（正例か負例を予測する場合）

分類問題で、正例か負例かを予測する問題で扱う評価関数について、まとめていきます。

混同行列

評価指標ではないですが、正例と負例を予測する評価指標で利用されるため、最初に説明します。

混同行列は、以下の分類結果を表形式で表します。

TP(True Positive) : 正例を正しく予測
TN(True Negative) : 負例を正しく予測
FP(False Positive) : 正例と誤って予測
FN(False Negative) : 負例と誤って予測

1from sklearn.metrics import confusion_matrix
2confusion_matrix(y_true, y_pred)

以下の形式で出力されます。

	予測値が負例	予測値が正例
真の値が負例	TN	FP
真の値が正例	FN	TP

Accuracy

正解率。予測結果全体に対して、予測が正しい割合を表します。

正解率(\textrm{Accuracy}) = \frac{TP + TN}{TP + TN + FP + FN}

1from sklearn.metrics import accuracy_score
2accuracy_score(y_true, y_pred)

Precision

適合率。正例と予測したなかで正しく予測できた割合を表します。

適合率(\textrm{Precision}) = \frac{TP}{TP + FP}

1from sklearn.metrics import precision_score
2precision_score(y_true, y_pred)

Recall

再現率。実際に正例のなかで正しく予測できた割合を表します。

再現率(\textrm{Recall}) = \frac{TP}{TP + FN}

1from sklearn.metrics import recall_score
2recall_score(y_true, y_pred)

F1-score

F値。 precisionとrecallのバランスをとった指標を表します。

precisionとrecallの調和平均で計算されます。

\textrm{F1-score} = \frac{2 \times \textrm{recall} \times \textrm{precision}}{\textrm{recall} + \textrm{precision}}

1from sklearn.metrics import f1_score
2f1_score(y_true, y_pred)

二値分類（正例である確率を予測する場合）

次に、分類問題で正例である確率を予測する問題で扱う評価関数についてまとめます。

logloss

cross entropyとも呼ばれることもあります。予測した確率分布と正解となる確率分布がどのくらい同じかを表します。

0から1の値をとる
正しく予測できているときに小さくなる

\begin{align} \textrm{logloss} &= -\frac{1}{N}\sum_{i=1}^{N}(y_{i}\log p_{i} + (1 - y_{i}) \log (1 - p_{i})) \nonumber \\ &=-\frac{1}{N}\sum_{i=1}^{N} \log \acute{p}_{i} \nonumber \end{align}

\begin{align} y_{i} &: 正例かどうか表すラベル \nonumber \\ p_{i} &: 正例である予測確率 \nonumber \\ \acute{p}_{i} &: 真の値を予測している確率 \nonumber \end{align}

1from sklearn.metrics import log_loss
2log_loss(y_true, y_prob)

AUC

ROC曲線の下部の面積を表します。

ランダムな予測は0.5
全て正しく予測すると1.0
不均衡データでの分類に利用
予測確率と正解となる値(1か0か)の関係から評価

1from sklearn.metrics import roc_auc_score
2roc_auc_score(y_true, y_prob)

ROC曲線とは

予測値を正例とする閾値を0から1に動かした時の真陽性率と偽陽性率の関係をプロットしたグラフです。閾値を変化させると真陽性率と偽陽性率がどのように変化するかを表します。

真陽性率：全体の正例のうち正例と予測した割合
偽陽性率：全体の負例のうち正例と予測した割合

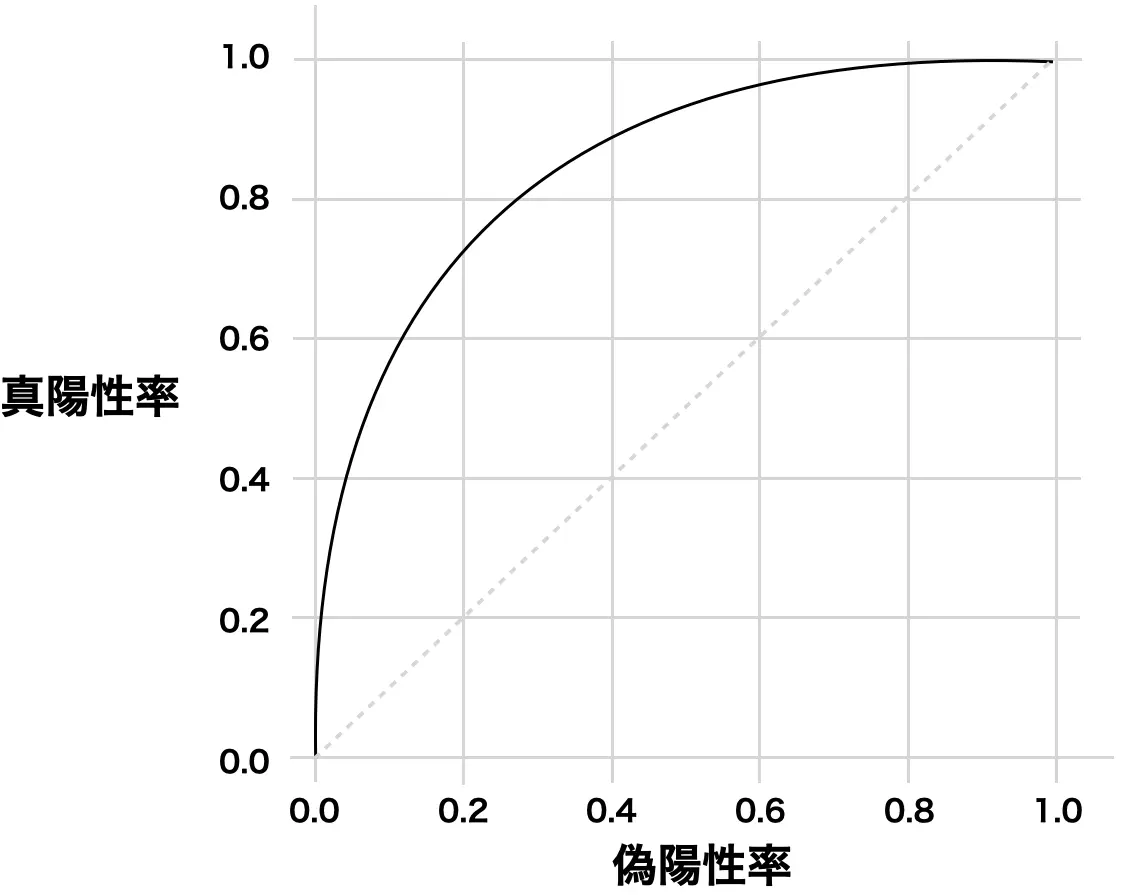
(1.0, 1.0)は全て正例と予測
(0.0, 0.0)は全て負例と予測
(0.0, 1.0)上は全て正しく予測
直線はランダムな予測（AUC=0.5)

多クラス分類

Multi-class accuracy

二値分類のAccuracyを多クラス分類に拡張した指標となります。正しく予測がされているレコード数の割合を表します。

1from sklearn.metrics import accuracy_score
2accuracy_score(y_true, y_pred)

mean-F1/macro-F1/micro-F1

F1-scoreを多クラス分類に拡張した指標となります。

mean-F1：レコードごとのF1-scoreの平均
macro-F1：クラスごとのF1-scoreの平均
micro-F1：レコード×クラスのペアごとにTP/TN/FP/FNを計算してF1-scoreを算出

1from sklearn.metrics import f1_score
2f1_score(y_true, y_pred, average='samples')
3f1_score(y_true, y_pred, average='macro')
4f1_score(y_true, y_pred, average='micro')

Multi-class logloss

二値分類のloglossを多クラス分類に拡張した指標となります。

\textrm{multiclass logloss} = -\frac{1}{N}\sum_{i=1}^{N}\sum_{m=1}^{M}y_{i,m}\log p_{i,m}

\begin{align} M :& クラス数 \nonumber \\ y_{i,m} :& レコードiがクラスmに属するか表すラベル \nonumber \\ p_{i,m} :& レコードiがクラスmに属する予測確率 \nonumber \\ \end{align}

1from sklearn.metrics import log_loss
2log_loss(y_true, y_prob)

参照

Amazonで見る

Support

\ この記事が役に立ったと思ったら、サポートお願いします！ /

Prophetで時系列データ予測

2021.06.27

NeuralProphetで時系列データ予測

2021.07.25

scikit-learnで正規分布へ変換

2022.08.07

【入門機械学習】動かして理解する人工知能・機械学習・ディープラーニングの違い

2021.05.16

Profile

Masa

都内のIT企業で働くエンジニア
自分が学んだことをブログでわかりやすく発信していきながらスキルアップを目指していきます！